Deep Dive with Leex and Yecc - Part 1
This is the first post in a series that show how to use Erlang’s leex and yecc to tokenize and parse strings in Elixir. Our case study will involve parsing dice rolling expressions and writing code that turns our parse trees into dynamic, reusable functions.
We are kicking off the series by describing dice rolls, the need for a dice-rolling DSL, and some basic considerations when creating our new DSL.
 Wooden Chtulhu dice tower.
Wooden Chtulhu dice tower.
Dice Rolls and Functions
Your character must pass a skill check to climb the wall. The climbing skill check requires rolling your skill die, an eight-sided die, and your ‘wild’ die, a six-sided die. Add two to both rolls and pick the highest value. If its greater than four, you succeed. Otherwise, you fall and die a horrific, mangled death.
What reads like a word problem in a high school math class run by geeks is a common occurence in role-playing games. In essence, you model a character’s capabilities with rules involving ranged randomized values with applied modifiers. If you were to look in the rulebook, you would find a shorthand version, “Roll a skill check of 1d8+2, 1d6+2. The result must be higher than 4 to succeed.”, where:
1d8or1d6: roll a number of dice, in this case1die, where each die has a specified number of sides, in this case a die with8sides and a die with6sides+2: add two to each dice roll, this is our modifier,: pick the highest of the two outcomes
How would you model this in code?
One option is to create functions that simulate dice rolls and apply our modifier to each roll. What would that look like? Fire up iex we’ll see:
iex(1)> d6 = fn -> Enum.random(1..6) end
#Function<20.99386804/0 in :erl_eval.expr/5>
iex(2)> d8 = fn -> Enum.random(1..8) end
#Function<20.99386804/0 in :erl_eval.expr/5>
iex(3)> d6_result = d6.()
4
iex(4)> d8_result = d8.()
5
iex(5)> wild_die_result = d6_result + 2
6
iex(6)> skill_die_result = d8_result + 2
7
iex(7)> result = if skill_die_result < wild_die_result do wild_die_result else skill_die_result end
7
iex(8)> if result > 4 do :skill_check_success else :skill_check_failed end
:skill_check_successThis models the word problem above, where we roll one eight-sided die (1d8) and one six-sided die (1d6). We add two (+2) to both results, pick the highest, and check to see if it’s greater than four. Looking at it again, we could write more generic functions that encapsulate a lot of this, letting us pass any number of dice and compare the results.
iex(1)> roll = fn num_dice, num_sides, modifier ->
...(1)> 1..num_dice
...(1)> |> Enum.map(fn _ ->
...(1)> Enum.random(1..num_sides) + modifier
...(1)> end)
...(1)> end
#Function<18.99386804/3 in :erl_eval.expr/5>
iex(2)> compare = fn roll_1, roll_2 ->
...(2)> if roll_1 > roll_2 do
...(2)> roll_1
...(2)> else
...(2)> roll_2
...(2)> end
...(2)> end
#Function<12.99386804/2 in :erl_eval.expr/5>
iex(3)> skill_check = fn [value_to_check], comparable ->
...(3)> IO.puts("roll: #{value_to_check}, comparable: #{comparable}")
...(3)> if value_to_check > comparable do
...(3)> :success
...(3)> else
...(3)> :failure
...(3)> end
...(3)> end
#Function<12.99386804/2 in :erl_eval.expr/5>
iex(4)> 1 |> roll.(8, 2) |> compare.(roll.(1, 6, 2)) |> skill_check.(5)
roll: 10, comparable: 5
:success
iex(5)> 1 |> roll.(8, 2) |> compare.(roll.(1, 6, 2)) |> skill_check.(8)
roll: 5, comparable: 8
:failureThis simplification definitely makes rolling dice and using basic modifiers easier. However, most rule-based systems in games or business have a multitude of specialized rules, combinations of rules, one-off edge cases, and more. Modeling each rule, even with some generic functions, would inevitably lead to an explosion of functions that must interrelate. For instance, what if we wanted to…
- add rolls of rolls using 2d6d8?
- compare several different rolls via 1d6+2, 1d6-1, 1d8+4, 1d10-5?
- or have more complex, nested equations like 3d8 + 2d10 / (1d6+2)?
We could simulate these equations by building a collection of reusable functions that would be called and combined throughout a slew of unique functions. But then each unique combination or setup would require the creation of more and more unique functions.
Wouldn’t it be nice if instead we wrote out and executed equations like those above, or the one mentioned in the word problem earlier? That would be far more concise, composeable, expressive, and would handle nesting quite nicely.
Domain-Specific Languages (DSL)
If we create a language specific to the domain of dice-rolling, with symbols that detail how things interact with one another, and a set of rules for those interactions, we’ll end up with a domain specific language, or DSL for short.
Real world examples of DSLs include the symbols and interactions in electrical engineering, the structure and rules of XML, and one that should be familiar to us all - the langauge/notation of math.
| Electrical Engineering | XML from Wikipedia Source | Carry Arithmetic |
|---|---|---|
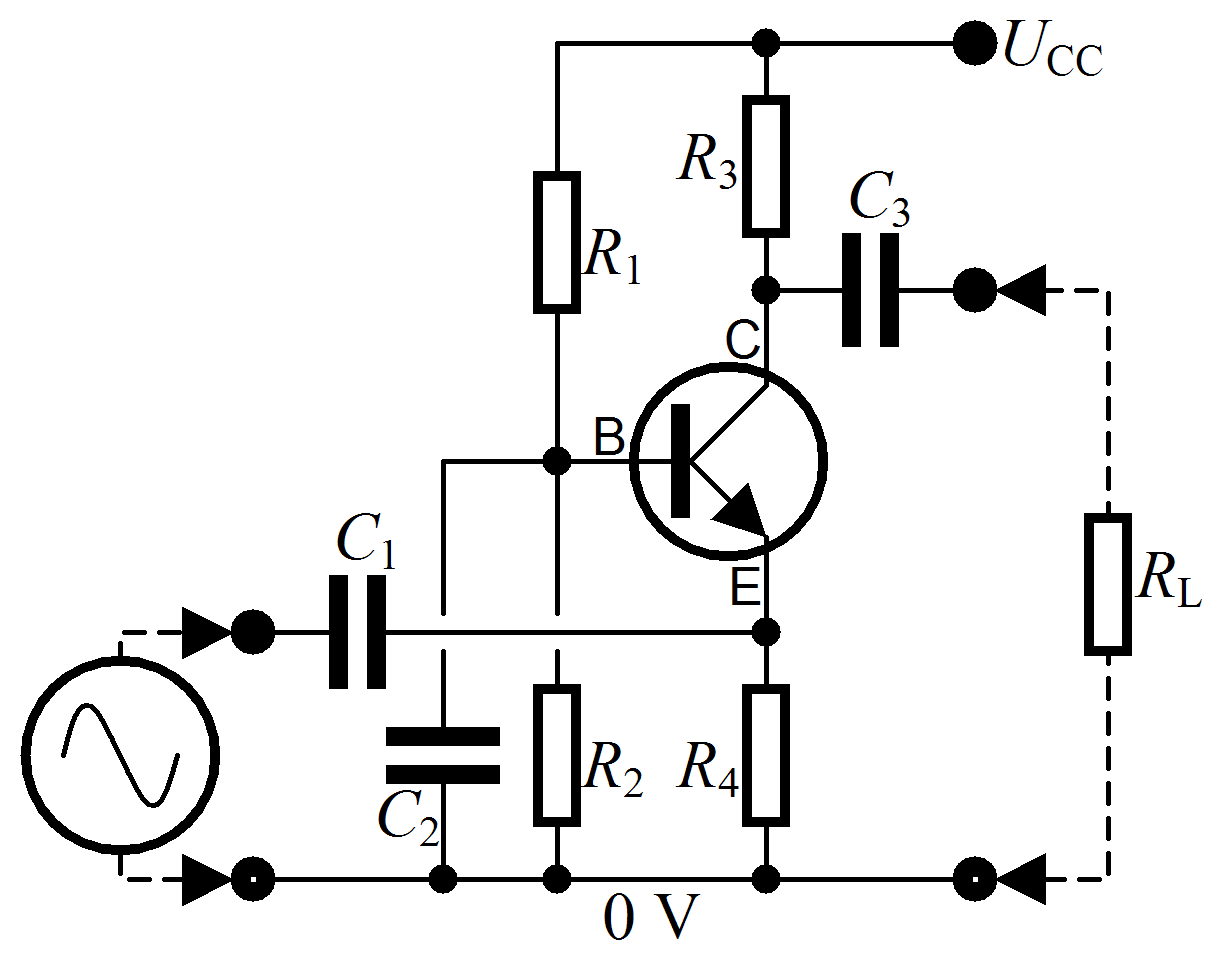 |
 |
 |
What should our dice-rolling language look like? To answer that question, we need to state a clear goal:
The goal of this dice-rolling langauge is to provide a familiar and concise means of expressing equations involving dice rolls.
The goal is broad, but we can infer the requirements. The end result must be capable of expressing equations, including those involving dice rolls. The language must express these equations in a manner that is familiar to the general population. The language must avoid verbosity while providing enough elements to express complex equations.
Inventing new languages is hard. If possible, it’s better to find and augment an existing language instead of building a brand new one from scratch. But that begs the question, “Are there any domain-specific languages that match these requirements?” The answer is yes, algebraic equations.
The Big Three Math Notations
Over the last few thousand years, humans have come up with a variety of symbols and notation styles for expressing mathemematical concepts and equations. Those languages, hereafter referred to as notations, have evolved over time to the few people commonly use today.
Infix notation (algebraic notation) is the most common and familiar DSL used for expressing arithemetic. While we could stop at infix, there are two other significant notations - prefix (Polish notation) and postfix (Reverse-Polish notation). Here’s a simple example of adding the numbers three and four together in each notation:
| Prefix | Postfix | Infix |
|---|---|---|
 |
 |
 |
The notations look quite similar, and in fact share the following traits:
- the basic symbols for numbers (operands) and calculations (operations)
- operands, or what we feed into the calculation, such as numbers, vectors, or other equations
- operations, or the actual calculations themselves, and their symbols, called operators
- having multiple categories of operations, though we only care to use the following two:
- binary operations - calculations that require two operands to work, such as addition and subtraction, whose operators are
+and-respectively - unary operations - calculations that require only one operand to work, such as the
-and+symbols in-3and+99.
- binary operations - calculations that require two operands to work, such as addition and subtraction, whose operators are
If the three main notations share these concepts, we should use them too. These concepts, and the symbols that represent them, fulfill part of our goal of using a notation that is familiar, concise, and expressive. In our next blog post, we will discuss tokenizing equations. The tokens we create will represent the symbols as described above. The post after that will focus on how to describe the relationship between them, otherwise known as the grammar.
However, though they share all of the above, they have definite differences in expression (again, grammar). Infix notation places the operator between the operands, as in 2 + 2. Prefix notation places the operator before its operands, like so + 2 2, and postfix places the operands before the operator, such that 2 2 +.
The differences appear cosmetic, but they have dramatic impacts in how they are processed. To illustrate this, let’s take the following algebraic word problem, break it down into individual math symbols, and convert them into the three notations:
Calculate the value of five minus six times negative seven plus three.
First, we convert the word problem into arithmetic symbols.
| Name | Symbol | Type | Category |
|---|---|---|---|
five |
5 |
operand | number |
minus |
- |
operator | binary operation |
six |
6 |
operand | number |
times |
* |
operator | binary operation |
negative |
- |
operator | unary operation |
seven |
7 |
operand | number |
plus |
+ |
operator | binary operation |
three |
3 |
operand | number |
We take these symbols (called tokens in programming) and convert them into the three styles of notation using their grammar rules:
| Notation | Example | Commutative Alternative |
|---|---|---|
| Infix | (5-6) * (-7+3) |
(3+-7) * (5-6) |
| Prefix | * - 5 6 + -7 3 |
* + 3 -7 - 5 6 |
| Postfix | 5 6 - -7 3 + * |
3 -7 + 5 6 - * |
Note how infix notation requires the use of parentheses to show how addition and subtraction must be performed before multiplication. If we don’t use parentheses, multiplication will be performed first due to operator precedence. Neither prefix nor postfix require disabmiguation because each operator and set of operands are performed in a particular direction whereas infix can be approached from any direction. Why is that? Because infix notation places operators between operands while prefix places operators before their operands and postfix places operators after their operands.
This is very imporant when it comes to working with computers, because they generally don’t like ambiguity. It is far more difficult to handle situations of ambiguity, and often requires more rules and instructions to avoid any misunderstandings. Therefore, while computers are programmed to interpret infix notation, it’s far easier to work with and manipulate the simpler structures of prefix and postfix notation.
So if prefix and postfix are better for computers, why bother with infix at all?
Because infix is the notation that is most adaptable to our goal:
The goal of this dice-rolling langauge is to provide a familiar and concise means of expressing equations involving dice rolls.
Infix it is. But, where does that leave postfix and prefix?
Postfix is great for memory conservation and immediate processing of a list of operands and operators. Going this route allows us to iterate over each character in an expression, place the operands in output, and manage operators on a tiny stack. It should come as no surprise that many people, when faced with parsing simple arithemetic expressions, will use the shunting-yard algorithm to convert infix to postfix and execute.1.
Prefix, on the other hand, is great for computer languages because it treats operators like functions whose arguments come immediately after. This means the expression + 2 2 can be more easily treated as +.(2, 2), which works great for pattern matching against strings. Also note that prefix notation is a lot like S-expressions in Lisp.2
When we reach the point of computing the result of our parsed equations, we’ll be working with a syntax tree whose root node is an operator with two child opeands. Each operand can be a number, or another operator with operand children of its own. As an example, after being parsed the expression (5-6) * (-7+3) will become:
{{:operator, '*'},
{{:operator, '-'}, 5, 6},
{{:operator, '+'}, -7, 3}
}Looks an awful lot like prefix notation, eh? We’ll revisit this when we focus on processing our parse trees from yecc. For now, let’s look at what we need to do to make infix our own. Let’s look back at two of our earlier dice-rolling expressions:
Customizing Infix Notation
Now that we’ve decided to use a modified form of infix, we can review any additions necessary to make it our own. Let’s return to two earlier examples to see what we can find:
- comparing several different rolls:
1d6+2, 1d6-1, 1d8+4, 1d10-5 - example of a nested expression:
3d8 + 2d10 / (1d6+2)
It would appear the difference is that we are adding two operators: one representing a dice roll (d); and another for comparing multiple expressions (,).
We’re adding two new operators, but how do they interact with other operators and operands? Reviewing how dice rolls are written, where 1d6 means rolling one six-sided die, we can safely say the d operator requires two operands. The same can be said of the comparison operator (,), where we state that both sides are to be compared to one another.
Since both operators require two operands, like addition, division, and others, they would be considered binary operations.
Great! We now have the conceptual framework for a dice-rolling DSL. Next, we need to figure out how we begin parsing these expressions into something actionable.
Up Next
In this post, we covered the need for a dice-rolling DSL, explored similar notations, and decided to customize infix with our specific needs. Part two of our dice rolling adventures will focus on using leex to convert dice roll equations into tokens based on our DSL.
Footnotes
-
For those interested, I threw together a bare-bones implementation of the algorithm for parsing dice roll expressions. ↩
-
We’ll be using S-expressions later, when we take our “code as data structure” and begin to execute on them. ↩