Deep Dive with Leex and Yecc - Part 2

This is the second post in a series about using Erlang’s leex and yecc in Elixir. In part one, we introduced dice rolling calculations and the need for a DSL to more easily translate those systems into functional code. We looked at various types of arithmetic notations systems to learn how we should structure our DSL, and ended up settling on one that is most familiar with the world at large - infix notation.

Today, we take our next step in the journey and learn how to use leex to tokenize our DSL.

Various dice in a 3-D printed dice tower.

Tokenizing with Leex

In the last post, we looked at how we convert a world problem “Calculate the value of five minus six times negative seven plus three,” into notation by identifying and writing down each symbol, then applying the notation’s grammar to it. Computers need to do the same, and they need instructions on how to do it. The first step in the process, identifying symbols, is called lexical analysis, and more specifically for us, tokenization.

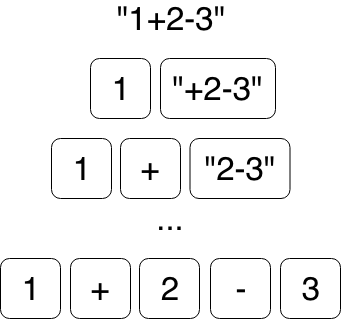Converting the string “1+2-3” into tokens.

Writing your own lexical analyzer can be painful, especially when you take into account all the edge cases and potential unknowns. That’s why many people turn to libraries that can generate lexical analyzers, known as lexer generators. Two of the most established lexer generators are lex and flex. Erlang has its own lexer generator, called leex, which operates very similar to lex and flex.

Generating Our First Lexer

Lexer generators have their own DSL that describes how text should be tokenized. Instead of describing how it all works, let’s generate one of our own and poke around:

1. create a new elixir project named dice_roller via mix new dice_roller
2. create a folder named src in the project’s root folder
3. create a file named dice_lexer.xrl in the src folder and open it in your editor of choice
4. type the following code into your editor and save your file:

Definitions.

Number          = [0-9]+
Operator        = \+

Rules.

{Number}            : {token, {int, TokenLine, TokenChars}}.
{Number}\.{Number}  : {token, {float, TokenLine, TokenChars}}.
{Operator}          : {token, {op, TokenLine, TokenChars}}.

Erlang code.

Boom, you have generated your very own number lexer! Now to take it for a spin. Start iex with iex -S mix run. Next, type "1" |> to_charlist() |> :dice_lexer.string() and hit enter. You should see something similar to the following:

Erlang/OTP 20 [erts-9.3.3.3] [source] [64-bit] [smp:12:12] [ds:12:12:10] [async-threads:10] [hipe] [kernel-poll:false] [dtrace]

Compiling 1 file (.xrl)
Compiling 1 file (.erl)
Compiling 1 file (.ex)
Generated dice_tosser app
Interactive Elixir (1.6.6) - press Ctrl+C to exit (type h() ENTER for help)
iex(1)> "1" |> to_charlist() |> :dice_lexer.string()
{:ok, [{:int, 1, '1'}], 1}
iex(2)>

It works! Notice the two lines talking about compiling the .xrl and .erl files? When you compile your project or run it, elixir compiles any erlang files in the src folder. Also, remember how leex is a lexer generator? The .xlr file is compiled and generates the lexer’s erlang (.erl) file. Finally, elixir compiles the .erl file and loads it as we start our application.

Now to poke around and explore the lexer itself…

> iex -S mix run
Erlang/OTP 20 [erts-9.3.3.3] [source] [64-bit] [smp:12:12] [ds:12:12:10] [async-threads:10] [hipe] [kernel-poll:false] [dtrace]

Interactive Elixir (1.6.6) - press Ctrl+C to exit (type h() ENTER for help)
iex(1)> "1" |> :dice_lexer.string()
** (FunctionClauseError) no function clause matching in :lists.sublist/2

    The following arguments were given to :lists.sublist/2:

        # 1
        "1"

        # 2
        1

    ...

iex(1)> "1" |> to_charlist() |> :dice_lexer.string()
{:ok, [{:int, 1, '1'}], 1}

iex(2)> lex_str = fn str -> str |> to_charlist() |> :dice_lexer.string() end
#Function<6.99386804/1 in :erl_eval.expr/5>

iex(3)> lex_str.("1")
{:ok, [{:int, 1, '1'}], 1}
iex(4)> lex_str.("123")
{:ok, [{:int, 1, '123'}], 1}

iex(5)> lex_str.("4.5")
{:ok, [{:float, 1, '4.5'}], 1}
iex(6)> lex_str.("+")
{:ok, [{:op, 1, '+'}], 1}

iex(7)> lex_str.("1+1")
{:ok, [{:int, 1, '1'}, {:op, 1, '+'}, {:int, 1, '1'}], 1}
iex(8)> lex_str.("1+1.2")
{:ok, [{:int, 1, '1'}, {:op, 1, '+'}, {:float, 1, '1.2'}], 1}

iex(8)> {:ok, tokens, _} = lex_str.("1+1.2")
{:ok, [{:int, 1, '1'}, {:op, 1, '+'}, {:float, 1, '1.2'}], 1}
iex(9)> tokens
[{:int, 1, '1'}, {:op, 1, '+'}, {:float, 1, '1.2'}]

iex(10)> lex_str.("1-1.2")
{:error, {1, :dice_lexer, {:illegal, '-'}}, 1}
iex(11)> lex_str.("")
{:ok, [], 1}

iex(12)> lex_str.(" ")
{:error, {1, :dice_lexer, {:illegal, ' '}}, 1}
iex(13)>

Interesting. So what did our brief exploration reveal?

• the leex file is compiled into a module with the same name as the file (i.e. :dice_lexer)
• we tokenize strings with our lexer by calling :dice_lexer.string/1
• the lexer succeeds with character lists but fails on strings
• the lexer can tokenize integers, floating point numbers, and the + operator
• the lexer cannot handle any other operators nor spaces
• the lexer returns a tuple {:ok, tokens, end_line_number}

Breaking Down the Leex File

We’ve generated our first lexer, used it to tokenize numbers and the + sign, and explored some of the edges. Now let’s go back and see how it all fits together. We’ll start with the leex file that now contains additional comments[^erlang info]:

% Everything between `Definitions.` and `Rules.` is a macro and value.
%
% Defintion Format:
% Macro         = Value
Definitions.

Number          = [0-9]+
Operator        = \+

% Everything betweeen `Rules.` and `Erlang code.` represent regular
% expressions transformed into erlang code. Note how they use the
% defintions from above.
%
% Rule Format:
% Regular Expression    : erlang code
Rules.

{Number}                : {token, {int, TokenLine, TokenChars}}.
{Number}\.{Number}      : {token, {float, TokenLine, TokenChars}}.
{Operator}              : {token, {op, TokenLine, TokenChars}}.

% Any erlang can be added here to assist processing in `Rules.`
Erlang code.

First, there are three things to note about working with erlang. Erlang function calls and statements end in a period (.). If you don’t use a period, your erlang code won’t compile. Also note that erlang specifies atoms the way elixir specifies variables. In the above, token, int, float, and op appear as :token, :int, and :float, and :op in elixir. Finally, erlang variables begin with a capital letter. Thus, the left hand side of each definition is a variable.

As noted in the comments above, each leex file is composed of three main sections

• Definitions are used to generate macro defintions, whose values are often regular expressions. In our case, a regular expression to capture numbers.
• Rules are a set of regular expressions that will, upon matching anywhere in the string, send the matched text to the erlang code on the right side of the rule’s : separator and generate tokens.
• Erlang code contains any erlang functions or the like used in this leex rule’s file.

Definitions are relatively simple, with the variable on the left and the value (e.g. regular expressions and constants) on the right. We won’t spend any more time on that. Also, we aren’t using any custom erlang code, so we’ll skip the last section. For now, we will focus on Token Rules.

Token Rules

Token rules are where the magic happens, so let’s dive in by breaking down the first rule into its pieces:

{Number} : {token, {int, TokenLine, TokenChars}}.

• {Number}: This references the Number definition, whose value was the regular expression [0-9]+.
• :: This separates the regular expression on the left and the erlang code on the right.
• {token, {int, TokenLine, TokenChars}} the erlang code that acts upon the found value, in our case a number

The regular expression on the left side of each rule is relatively simple. You combine defintions and strings into regular expressions. In our case, our first rule looks for numbers using {Number}. In the second rule, we find floating point values using the regular expression {Number}\.{Number}, while the third is used to grab any operators, which for now is only +. However, the right hand side of each rule has a bit more going on.

Token Rules can only return the following values:

• {token, Token}: returns a token consisting of the text matched in the regular expression
• {end_token, Token}: returns a token, but also serves as a way of saying this is the last token
• skip_token: skips the token entirely and is great for filtering out spaces and more
• {error, ErrString}: an error string is returned

When returning a token, leex provides three predefined variables:

• TokenChars: characters matched by this rule
• TokenLen: number of matched characters
• TokenLine: line number of matched characters

Armed with this knowledge, we can now investigate the right hand side of each rule.

{Number}                : {token, {int, TokenLine, TokenChars}}.
{Number}\.{Number}      : {token, {float, TokenLine, TokenChars}}.
{Operator}              : {token, {op, TokenLine, TokenChars}}.

• {token, _}: this tells leex we are returning a token
• int, float, op: this atom identifies the type of data in this token tuple
• TokenLine: the line number of this token
• TokenChars: the characters matched by this rule

Adding more Token Rules

To reinforce how leex rules work, we’ll add another operation to our DSL - dice rolling. When adding a rule to leex, the high-level steps are the same:

1. add or change defintions to accommodate the new token
2. create a token rule that tells the lexer how to tokenize the expression
3. verify our rules through testing edge cases

Dice Rolling Operator

The first step in adding a new rule is deciding if we need to add a new defintion, or change an existing definition. Dice rolling is an operation, and has its own operator (‘-‘). Looking over our existing definitions, we find:

Operator        = \+

Looks like we already have a defintion for operators, and the regular expression used matches our idea of an operator (+). Therefore, we’ll change this existing definition by adding the dice rolling operator (d):

Operator        = [\+d]

Easy enough. Now to take it for a spin.

iex(1)> lex_str = fn str -> str |> to_charlist() |> :dice_lexer.string() end
#Function<6.99386804/1 in :erl_eval.expr/5>
iex(2)> lex_str.("1d2")
{:ok, [{:int, 1, '1'}, {:op, 1, 'd'}, {:int, 1, '2'}], 1}
iex(3)> lex_str.("1+2d3")
{:ok,
 [{:int, 1, '1'}, {:op, 1, '+'}, {:int, 1, '2'}, {:op, 1, 'd'}, {:int, 1, '3'}],
 1}
iex(4)> lex_str.("1 + 2 d 3")
{:error, {1, :dice_lexer, {:illegal, ' '}}, 1}
iex(5)>

No surprises here, the dice rolling operator (d) reacts the same as addition. However, the last expression we tried had spaces, which failed. If we are going to make a DSL that’s familiar, we need to handle spaces.

Skipping Spaces

While spaces have no bearing on the outcome of a calculated equation, people often add them to their algebraic equations to improve readability. Compare the examples of following equation, one with spaces the other without:

• 5+6d(4+3^5/(1d4))+(5+1d4)d(4d6)
• 5 + 6d(4+3^5 / (1d4)) + (5+1d4)d(4d6)

If we are going to make a DSL that feels familiar, we’ll have to take spaces into account. Fortunately, leex provides an easy way to strip them out:

Definitions.

Number          = [0-9]+
Operator        = [\+d]
Space           = [\s\r\n\t]+

Rules.

{Number}            : {token, {int, TokenLine, TokenChars}}.
{Number}\.{Number}  : {token, {float, TokenLine, TokenChars}}.
{Operator}          : {token, {op, TokenLine, TokenChars}}.
{Space}             : skip_token.

Erlang code.

Trying it out:

iex(1)> lex_str = fn str -> str |> to_charlist() |> :dice_lexer.string() end
#Function<6.99386804/1 in :erl_eval.expr/5>
iex(2)> lex_str.("1 + 2\n d 3")
{:ok,
 [{:int, 1, '1'}, {:op, 1, '+'}, {:int, 1, '2'}, {:op, 2, 'd'}, {:int, 2, '3'}],
 2}
iex(3)> lex_str.("\t 1 + 2\n d 3")
{:ok,
 [{:int, 1, '1'}, {:op, 1, '+'}, {:int, 1, '2'}, {:op, 2, 'd'}, {:int, 2, '3'}],
 2}
iex(4)>

As mentioned earlier in the post, leex can return tokens, including a special one named skip_token. This tells leex to drop this token and continuing tokenizing the rest of the string.

Handling Parentheses

Next up are parentheses. Infix uses them to group expressions that should be calculated before others. This means we need to know the boundaries of a parenthetical expression. In that case, we should have separate tokens for left (() and right ()) parentheses:

Definitions.

Number          = [0-9]+
Operator        = [\+d]
Space           = [\s\r\n\t]+
LeftParen       = \(
RightParen      = \)

Rules.

{Number}            : {token, {int, TokenLine, TokenChars}}.
{Number}\.{Number}  : {token, {float, TokenLine, TokenChars}}.
{Operator}          : {token, {op, TokenLine, TokenChars}}.
{Space}             : skip_token.
{LeftParen}         : {token, {'(', TokenLine, TokenChars}}.
{RightParen}        : {token, {')', TokenLine, TokenChars}}.

Erlang code.

and trying it out:

iex(1)> lex_str = fn str -> str |> to_charlist() |> :dice_lexer.string() end
#Function<6.99386804/1 in :erl_eval.expr/5>
iex(2)> lex_str.("1+(2d3)")
{:ok,
 [
   {:int, 1, '1'},
   {:op, 1, '+'},
   {:"(", 1, '('},
   {:int, 1, '2'},
   {:op, 1, 'd'},
   {:int, 1, '3'},
   {:")", 1, ')'}
 ], 1}
iex(3)>

You’ll notice that we use the parenthetical characters themselves instead of another named atom. The reason for this will become more apparent when we work with yecc.

Adding Other Operators

The other operators we care about include multiplication (*), division (/), and subtraction (-). Instead of doing all the work here, I leave that up to the reader. If you get stuck, I’ve put up a github repo with the final leex file and an example module using it.

Up Next

Using leex, we can convert our dice roll symbols into actual tokens. We start by creating defintions of the basic elements. Next, we create rules that use our definitions to interpret one or more characters in a string and convert them into token tuples. Now that we have our token tuples, we need to apply a grammar to them.

In the third blog post of the series, we will investigate taking our tokens and applying the grammar of our DSL to them using erlang’s yecc.